Loi binomiale
Définition : Loi binomiale
On appelle Loi binomiale de paramètres \(n\) et \(p\), la loi de probabilité de la variable aléatoire qui associe au schéma de Bernoulli de paramètres \(n\) et \(p\) le nombre \(k\) de succès.
Nb \(k\) de succès | \(0\) | \(1\) | ... | \(n\) |
|---|---|---|---|---|
\(P(X=k)\) | \(P(X=0)\) | \(P(X=1)\) | ... | \(P(X=n)\) |
La Loi binomiale de paramètres \(n\) et \(p\) est notée \(B(n,p)\).
Exemple : Loi binomiale B(2 ;p)
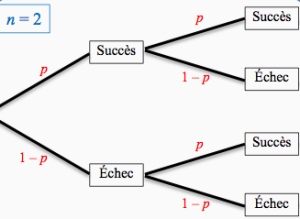
Pour 0 succès, il n'y a qu'un chemin :
\(P(X=0)=(1-p)\times (1-p)=(1-p)^2\).
Pour 1 succès, il y a deux chemins :
\(P(X=1)=(1-p)\times p + p\times (1-p)=2p(1-p)\)
Pour 2 succès, il n'y a qu'un chemin :
\(P(X=2)=p\times p=p^2\)
\(k\) | \(0\) | \(1\) | \(2\) |
|---|---|---|---|
\(P(X=k)\) | \((1-p)^2\) | \(2p(1-p)\) | \(p^2\) |
On peut vérifier que
\(P(X=0)+P(X=1)+P(X=2)=1\)
en développant le membre de gauche.