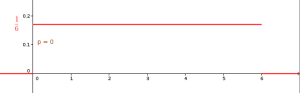
Définition de la loi uniforme
La loi uniforme se caractérise par une répartition uniforme des valeurs prises par une variable aléatoire continue sur un intervalle [a ;b]. Dès lors, sa fonction de densité est constante sur [a ;b] et nulle en dehors de cet intervalle puisque X n'y prend pas de valeurs.
La valeur de cette constante ne peut être choisie au hasard puisque la fonction de densité f(x) doit vérifier \(\displaystyle \int_a^b f(x)~dx=1\).
Si \(f(x)=k\) pour tout \(x\in[a ;b]\), alors on doit avoir \(\displaystyle \int_a^b k~dx=k\times (b-a)=1\) donc la valeur prise par la fonction de densité est nécessairement égale à \(\dfrac{1}{b-a}\) afin d'avoir une aire totale délimitée sur \([a ;b]\) égale à1.
Définition :
Soit a et b deux réels tels que \(a<b\).
Dire qu'une variable aléatoire continue X suit la loi uniforme sur \([a ;b]\) signifie que sa densité f est définie sur \(\mathbb R\) par :
\(\left\{\begin{array}{ l}\dfrac{1}{b-a}~\text{si }~x\in[a ;b]\\\\0~\text{sinon}\end{array}\right.\)
Si X suit la loi uniforme sur \([a ;b]\), on note \(X \hookrightarrow \mathcal U[a ;b]\).
Méthode : Calculer avec la loi uniforme
Si \(X \hookrightarrow \mathcal U[a ;b]\) ,
alors \(\mathbb P(c\leqslant X\leqslant d)=\displaystyle \int_c^d \dfrac{1}{b-a}~dx=\left[\dfrac{x}{b-a}\right]_c^d=\dfrac{d-c}{b-a}\)
Exemple :
Si \(X \hookrightarrow \mathcal U[0,5 ;2,5]\), on a \(\mathbb P(1\leqslant X\leqslant 1,5)=\dfrac{1,5-1}{2,5-0,5}=0,25\)
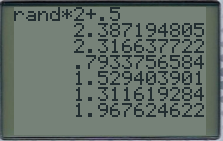
Pour simuler une telle variable aléatoire à la calculatrice, on utilise la fonction rand ou NbrAleat qui se trouve sur TI sous \(\fbox{MATH}~\fbox{PRB}\) ou sur Casio la fonction Ran# sous \(\fbox{OPTN}~\fbox{F6}~\fbox{F3}~PROB\).
Cette fonction renvoyant un nombre sur [0 ;1], on multiplie ce nombre par l'amplitude \((b-a)\) de l'intervalle, donc ici par 2 pour obtenir un nombre dans [0 ;2], puis on ajoute 0,5 afin de se ramener dans l'intervalle [0,5 ;2,5].
Sur le tableur, on saisira donc la formule \(\fbox{=2*ALEA()+0,5}\)