Loi de probabilité à densité
Définition :
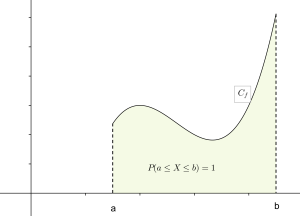
Soit \(f\) une densité de probabilité sur un intervalle \([a ;b]\).
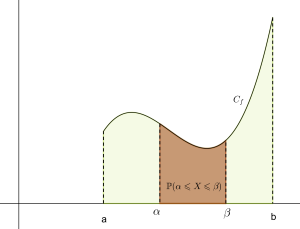
Une variable aléatoire X à valeurs dans un intervalle \([a ;b]\) suit la loi de densité \(f\) lorsque pour tous nombres α et β dans \([a ;b]\), on a :
\(\mathbb P(\alpha\leqslant X \leqslant \beta)=\displaystyle \int_\alpha^\beta f(x)~dx\)
Dans ce cas, la variable aléatoire est dite continue.
L'aire du domaine \(\left \{ M(x ;y) ;x\in [a;b] ~et ~0\le y\le f(x) \right \}\) est égal à 1.
\(\mathbb P(\alpha\leqslant X \leqslant \beta)\) est égale à l'aire du domaine \(\left \{ M(x ;y) ;x\in [\alpha;\beta] ~et ~0\le y\le f(x) \right \}\)
Exemple :
Dans le cas d'une variable aléatoire suivant la loi de densité de l'exemple précédent \(f(x)=3x^2\) sur \([0 ;1]\), on a :
\(\mathbb P(\dfrac{1}{4}\leqslant X\leqslant \dfrac{3}{4})=\displaystyle \int_{1/4}^{3/4}3x^2~dx=\dfrac{13}{32}\)
\(\mathbb P(X> \dfrac{1}{2})=\displaystyle \int_{1/2}^{1}3x^2~dx=\dfrac{7}{8}=0,875\)
Cette dernière probabilité peut s'interpréter à l'aide du graphique suivant :
Exemple :
La variable aléatoire donnant la taille d'une personne en cm est une variable aléatoire continue.
Complément :
Dans le cas où la variable aléatoire X est continue à valeurs dans un intervalle \([a ;+\infty[\), on doit s'assurer que la limite de l'aire d'un certain domaine tend vers 1 :
\(\displaystyle\lim_{x\rightarrow +\infty} \int_{a}^{x}f(t)~dt=1\)
On peut aussi définir de la même façon une variable aléatoire à valeurs dans un intervalle \(]-\infty ;a[\), ou bien encore sur \(]-\infty ;+\infty[\) en découpant le domaine en deux parties et en vérifiant que :
\(\displaystyle\lim_{x\rightarrow -\infty} \int_{x}^{0}f(t)~dt+\displaystyle\lim_{x\rightarrow +\infty} \int_{0}^{x}f(t)~dt=1\)