Définition
Définition :
On peut reconnaître une fonction continue sur un intervalle I par le fait que le tracé de sa courbe représentative sur cet intervalle peut se faire sans lever le crayon.
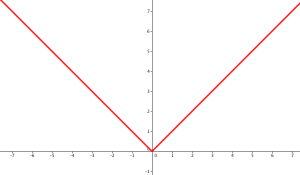
Exemple : Fonction valeur absolue
Cette fonction est définie pour tout réel et est continue sur \(\mathbb{R}\) car même en 0 où se produit un changement de forme, on peut ne pas lever le crayon lors du tracé.
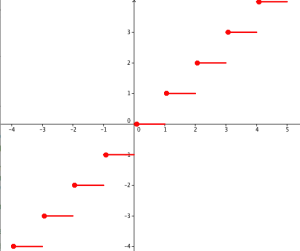
Exemple : Partie entière
La fonction partie entière n'est pas continue pour chaque valeur de x entière. Elle forme ce qu'on appelle une fonction en escalier.
Elle est par contre continue sur « chaque marche »
, c'est à dire sur chaque intervalle \([n ;n+1[\) où \(n\in \mathbb{N}\). Pour chaque valeur entière, un gros point sur la courbe indique la valeur effectivement prise par la fonction pour éviter toute ambiguïté de lecture graphique.