Définir une fonction continue sur un intervalle
Une fonction f est définie sur l'intervalle [0 ;+∞[ par \(f(x)=e^x\).
On souhaite définir sur \(]-\infty~;~0[\) la fonction f par une expression du type \(f(x)=-x+p\) où p est un réel à déterminer.
L'animation ci-dessous illustre le probléme en fonction des valeurs de p.
Question
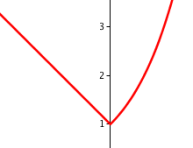
En vous aidant de l'animation ci-dessus, lire graphiquement pour quelle valeur de p la fonction est continue sur \(\mathbb{R}\).
Solution
En déplaçant le curseur, on s'aperçoit que pour \(p=1\), la fonction semble bien être continue.
Question
Retrouver la valeur de \(p\) par le calcul pour laquelle la fonction \(f\) est continue sur \(\mathbb{R}\)
Indice
La valeur de \(f\) en 0 doit être identique pour les deux expressions définissant la fonction.
Solution
Pour que la fonction soit continue en 0, il faut que \(-x+p\) ait en 0 la même valeur que \(e^x\) d'où l'équation : \(-0+p=e^0\) qui nous donne directement le résultat cherché : \(p=1\).
Par conséquent la fonction \(f\) définie par :
f(x)=e^x si x≥0
f(x)=-x+1 si x<0
est continue sur \(\mathbb{R}\).