Définition
Définition : Convexité et concavité
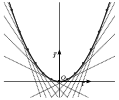
Dire qu'une fonction dérivable sur un intervalle est convexe sur cet intervalle signifie que sa courbe représentative est entièrement située au-dessus de chacune de ses tangentes.
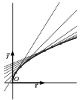
Dire qu'une fonction dérivable sur un intervalle est concave sur cet intervalle signifie que sa courbe représentative est entièrement située au-dessous de chacune de ses tangentes.
|
|
Fonction concave : la courbe est en dessous des tangentes | Fonction convexe: la courbe est en dessus des tangentes |
