Signe d'un quotient
Méthode :
La règle des signes énoncée au chapitre précédent reste valable avec les quotients.
La méthode est donc toujours d'établir un tableau de signes.
Il faut cependant être vigilant sur la valeur interdite. Celle-ci est figurée dans le tableau au moyen d'une double barre verticale.
Exemple :
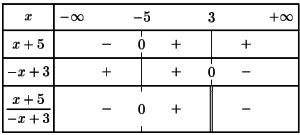
Déterminer le signe de \(f(x)=\dfrac{x+5}{-x+3}\).
On commence par chercher les valeurs de x qui annulent numérateur et dénominateur en résolvant :
\(x+5=0\) donc \(x=-5\)
\(-x+3=0\) donc \(x=3\). C'est la valeur interdite.
On inscrit dans un tableau les signes de chaque facteur du premier degré et on applique la règle des signes sur le quotient.
Le signe se lit alors dans la dernière ligne.
Ainsi \(f(x)\leq0\) si \(x\in]-\infty ;-5] \cup ]3 ;+\infty[\)
\(f(x) \geq0\) si \(x\in[-5 ;3[\)
Attention :
Comme pour le tableau de signe d'un produit, on prêtera attention au sens des crochets.
On sera toujours vigilant a systématiquement exclure des intervalles la valeur interdite.