La règle des signes
Fondamental :
Le produit (ou quotient) de deux nombres de même signe est positif.
Le produit (ou quotient) de deux nombres de signe contraire est négatif.
Cette règle s'avère intéressante pour résoudre des inéquations se présentant sous forme de produit de facteurs. On utilise pour cela un tableau de signes.
Exemple :
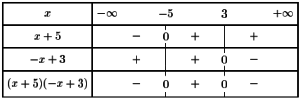
Déterminer le signe de \(f(x)=(x+5)(-x+3)\)
On commence par chercher les valeurs de x qui annulent f(x) en résolvant :
\(x+5=0\) donc \(x=-5\)
\(-x+3=0\) donc \(x=3\)
On inscrit dans un tableau les signes de chaque facteur du premier degré et on applique la règle des signes sur le produit.
Le signe se lit alors dans la dernière ligne.
Ainsi \(f(x)<0\) si \(x\in]-\infty ;-5[ \cup ]3 ;+\infty[\)
\(f(x) \geq0\) si \(x\in[-5 ;3]\)
Attention : Attention au sens des crochets
On sera très vigilant sur le sens des crochets. En effet, si l'égalité est stricte, on veillera à exclure la valeur de x qui annule le produit.