Système de deux équations à deux inconnues
Résoudre le système d'équation \((S) \left \{ \begin{array}{c}ax+by=c\\a'x+b'y=c'\end{array} \right.\), c'est trouver tous les couples (x,y) qui vérifient simultanément les deux équations
Comme les solutions de chacune des deux équations peuvent être représentées par des droites, la solution du système correspond aux coordonnées de l'intersection des deux droites.
Fondamental : Solutions possibles d'un système de deux équations à deux inconnues
Trois cas sont possibles :
les droites sont sécantes, le système admet un unique couple (x, y) comme solution.
les droites sont strictement parallèles, le système n'a pas de solutions.
les droites sont confondues (les deux équations sont alors équivalentes), le système a une infinité de solutions représentées par la droite.
Exemple : Résolution graphique d'un système de deux équations à deux inconnues
Considérons le système \((S) \left \{ \begin{array}{c}2x+y=5\\3x-2y=1\end{array} \right.\)
La première équation se réduit à l'équation \(y=-2x+5\).
La seconde équation se réduit à l'équation \(y=\dfrac{3}{2}x-\dfrac{1}{2}\).
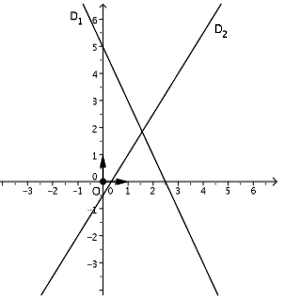
Les droites \((d_1) : y=-2x+5\) et \((d_2) : y=\dfrac{3}{2}x-\dfrac{1}{2}\) n'ont pas le même coefficient directeur donc elles sont sécantes.
Le système (S) admet donc une solution unique.
Graphiquement, les coordonnées du point d'intersection \((d_1) \cap (d_2)\) fournissent la solution du système. On lit sur le graphique ci contre que \(x\approx 1,6\) et \(y\approx 1,9\)