Modéliser une situation par un arbre
Un arbre permet de modéliser une situation et de déterminer une probabilité dans le cas où on étudie plusieurs événements.
Il est particulièrement bien adapté à la répétition d'expériences, aux situations où il y a plus de deux expériences et au cas où les expériences élémentaires ne sont pas équiprobables.
Dans le cas de deux expériences simultanées équiprobables, il vaut mieux utiliser un tableau.
Exemple :
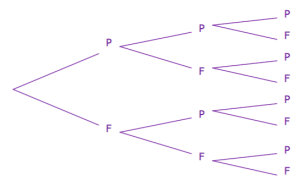
On lance trois fois une pièce et on regarde si on obtient pile (P) ou face (F).
Modéliser la situation par un arbre.
En déduire la probabilité d'avoir exactement une fois pile.
Il y a trois branches avec un seul pile pour un total de 8 branches donc la probabilité d'avoir exactement une fois pile est de 3/8 = 0,375
Complément : Arbre pondéré
Si l'arbre n'est pas pondéré, les événements décrits par une branche sont équiprobables. Sinon leur probabilité est égale au produit des branches.
Les événements étant disjoints les probabilités de chaque branche peuvent s'additionner.
Exemple :
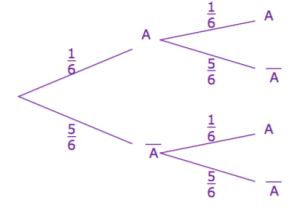
On lance 2 fois un dé équilibré et on s'intéresse à l'événement \(A\) : « Le nombre est 6 » et à son contraire \(\bar A\) .
Modéliser la situation par un arbre pondéré.
Quelle est la probabilité d'obtenir un 6 la deuxième fois seulement ?
La probabilité d'obtenir un 6 la deuxième fois seulement est la probabilité \(P(\bar A A)\).
En lisant la branche qui correspond, on voit que \(P( \bar A A)=\dfrac 5 6 \times \dfrac 1 6 = \dfrac 5{36}\).
