Utiliser un arbre pondéré
Une urne contient 5 boules rouges et deux blanches. On tire une boule on note sa couleur et on la remet puis on en tire une autre et on note sa couleur.
Question
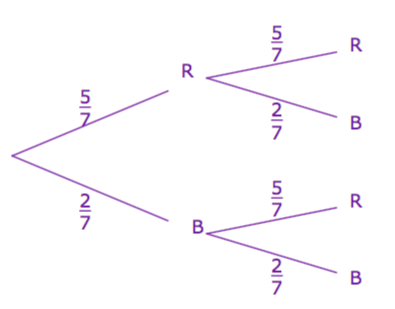
Représenter cette expérience par un arbre pondéré.
Question
Quelle est la probabilité d'avoir une boule blanche puis une rouge (probabilité notée \(P(BR)\)) ?
Solution
On calcule le produit des probabilités sur les branches. On a donc \(P(BR)=\dfrac 2 7\times \dfrac 5 7=\dfrac{10}{49}\)
Question
Quelle est la probabilité d'avoir tiré deux boules de couleur différente ?
Solution
On a tiré une Rouge puis une Blanche ou bien une Blanche puis une Rouge.
On cherche donc la probabilité de l'événement \((BR\cup RB)\), sachant que BR et RB sont incompatibles puisque sur des feuilles différentes de l'arbre.
\(P(BR\cup RB)=P(RB)+P(BR)\) car les événements RB et BR sont incompatibles, Il nous faut donc calculer P(RB) et P(BR) :
\(P(RB)=\dfrac 5 7\times \dfrac 2 7=\dfrac{10}{49}\)
Et \(P(BR)=P(RB)=\dfrac{10}{49}\)
Au final, la probabilité d'avoir tiré deux boules de couleur différentes est \(\dfrac{10}{49}+\dfrac{10}{49}=\dfrac{20}{49}\)