Rappels et définitions
Définition :
Un sous-ensemble de n individus dans une population constitue un échantillon de taille n.
Remarque :
Une méthode possible pour prélever un échantillon de taille n consiste à prélever au hasard et simultanément n individus d'une population. C'est ce qu'on appelle un échantillon aléatoire et exhaustif.
On étudie un caractère sur les individus d'un échantillon en vue de fournir une information sur la population toute entière.
Définition :
On appelle échantillonnage le prélèvement d'un échantillon dans une population.
Remarque :
 | Soit une population pour laquelle la proportion d'un caractère est p. On extrait au hasard un échantillon de taille n et on note f la fréquence de ce caractère dans l'échantillon. Cette fréquence est obtenue en divisant le nombre d'individus de l'échantillon présentant le caractère par n. La fréquence f peut varier d'un échantillon à l'autre et n'est pas nécessairement égale à la probabilité p du caractère. C'est ce qu'on appelle la fluctuation d'échantillonnage. |
Méthode : Rappel de seconde
On considère un caractère ayant une proportion
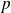dans une population donnée. On considère des échantillons de taille
dans cette population.
Si
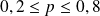et si
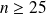alors la probabilité que la fréquence du caractère dans un échantillon appartienne à l'intervalle
est de 0,95. Ce qui signifie intuitivement que 95% au moins des échantillons sont tels que la fréquence du caractère appartient à l'intervalle précédent.
Remarque :
Plus la taille de l'échantillon est grande et plus la fréquence observée dans l'échantillon est proche de la proportion dans la population.
Exemple :
D'après l'Insee, la proportion de femmes dans la population française est d'environ 51,6 %.
● Si on observe des échantillons de 100 personnes représentatifs de cette population, alors 95 % d'entre eux doivent correspondre à une fréquence se trouvant dans l'intervalle de fluctuation au seuil de 95 %.
On a p = 0,516 et n = 100. L'intervalle de fluctuation au seuil de 95% est alors :
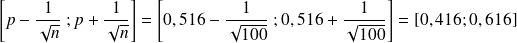
● Si on observe des échantillons de 1000 personnes l'intervalle de fluctuation au seuil de 95 % est alors :
soit environ [0,484 ; 0,548]
● Si on observe des échantillons de 10000 personnes l'intervalle de fluctuation au seuil de 95 % est alors :
