Estimation vote
Une estimation donne 30 % des intentions de vote à une personne politique que l'on appellera A.
On interroge un échantillon de 50 personnes et on admet que les réponses successives correspondent à un schéma de Bernoulli. On note N le nombre de personnes interrogées qui déclarent vouloir voter pour A.
1°) Quels sont les paramètres de la loi binomiale associée à N.
2°) Calculer la probabilité que 4 personnes exactement sur les 50 déclarent vouloir voter pour A et en donner une valeur approchée.
3°) Calculer la probabilité que 45 personnes exactement sur les 50 déclarent vouloir voter pour A et en donner une valeur approchée.
Dans toute la suite on utilisera une feuille de tableur.
4°) Entrer dans la plage A1:A51 les nombres entiers de 0 à 50.
Dans la cellule B1 entrer la formule =LOI.BINOMIALE(A1;50;0,3;0) donnant la probabilité de l'événement (N = 0). (0 correspond à la valeur contenue dans la cellule A1)
Recopier cette formule sur la plage B2:B51 pour obtenir P(N = k) pour tout entier k avec
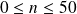 .
.
On vérifiera les valeurs obtenues dans les questions 2 et 3.
5°) Dans la cellule C1 entrer la formule =B1
Dans la cellule C2 entrer la formule =C1+B2
Recopier cette formule vers le bas jusqu'en C51.
À quoi correspondent les valeurs contenues dans la colonne C ?
6°) Déterminer le plus petit entier a tel que
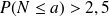 % .
% .
7°) Déterminer le plus petit entier b tel que
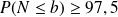 % .
% .
8°) Justifier que
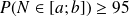 % .
% .
9°) Donner l'intervalle de fluctuation au seuil de 95% lorsqu'on interroge 50 personnes à propos de leur vote pour A. Comparer avec les valeurs précédentes.