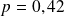Lien avec la loi binomiale
Fondamental :
Si un échantillon de taille n est prélevé au hasard dans une population présentant un caractère avec une probabilité p, alors le nombre d'individus de l'échantillon présentant le caractère étudié suit une loi binomiale de paramètres n et p.
Complément :
En effet, on peut assimiler le prélèvement d'un échantillon de taille n à n répétitions d'une même expérience de Bernoulli de probabilité p.
En pratique, si le rapport entre la taille de l'échantillon et la taille totale de la population est inférieur à 10%, un prélèvement successif sans remise pourra être assimilé à un tirage avec remise et donc conduira à une loi binomiale.
Exemple :
Dans une entreprise, 42% des employés utilisent le vélo pour se rendre au travail.
On interroge au hasard 10 employés et on note X la variable aléatoire qui compte le nombre k d'employés qui se rendent au travail à vélo.
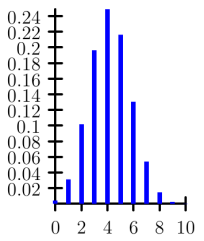 | La loi de probabilité de X est la loi binomiale de paramètres
Le diagramme ci-contre représente la loi de X. |
k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
p(X=k) | 0,004 | 0,031 | 0,102 | 0,196 | 0,249 | 0,216 | 0,130 | 0,054 | 0,015 | 0,002 | 0,001 |