Règle de décision
Méthode :
On considère l'hypothèse qu'un caractère se présente dans une population avec une proportion p.
On observe, sur un échantillon de taille n, la fréquence f de ce caractère.
On détermine l'intervalle de fluctuation au seuil de 95 % de la loi binomiale B(n ; p) :
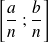
Si la fréquence observée f appartient à l'intervalle de fluctuation, on accepte l'hypothèse sur p avec une probabilité de 95%.
Si la fréquence observée f n'appartient pas à l'intervalle de fluctuation, on rejette l'hypothèse sur p avec une probabilité de 5% de se tromper.
Exemple :
Exemple
On émet l'hypothèse qu'un caractère se présente dans une population avec une proportion de 0,516.
On observe, sur un échantillon de taille 50, la fréquence de ce caractère et on trouve f = 0,4.
On se pose la question de savoir si cette fréquence est "compatible" avec l'hypothèse émise.
On considère le diagramme à barres ci-dessous représentant la loi binomiale B(50 ; 0,516).
On peut justifier (en utilisant un de tableur par exemple) que l'intervalle de fluctuation au seuil de 95 %
est obtenu avec a = 19 et b = 33, c'est donc l'intervalle :
.
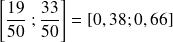Cet intervalle est obtenu en "rejetant" les valeurs inférieures à a (et correspondant à une probabilité
de 2,5 %) et les valeurs supérieures à b (et correspondant à une probabilité de 2,5 %).
La fréquence observée
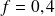se trouve dans l'intervalle de fluctuation au seuil de 95 %, l'hypothèse selon
laquelle le caractère se présente avec une proportion de 0,516 n'est pas rejetée.
Remarque :
Plus la taille de l'échantillon sera grande, plus l'intervalle de fluctuation sera restreint.
Avec l'exemple ci-dessus, l'intervalle de fluctuation au seuil de 95 % est :
● [0,38 ; 0,66] pour un échantillon de taille 50 ;
● [0,42 ; 0,61] pour un échantillon de taille 100 ;
● [0,485 ; 0,55] pour un échantillon de taille 1000.
