Les boîtes
Une société fabrique des boîtes en plastique de deux couleurs : des vertes et des bleues.
La fabrication est automatisée et la machine est réglée à un niveau de 42 % de boîtes vertes et 58 % de boîtes bleues, correspondant à la demande du marché.
Un test est fait sur un échantillon de 180 boîtes prélevées au hasard.
Question
L'échantillon comporte autant de boîtes bleues que de boîtes vertes. La machine est-elle déréglée ?
À partir de combien de boîtes bleues et de boîtes vertes obtenues sur un échantillon de 180 boîtes doit-on penser que la machine s'est déréglée ?
La proportion de boîtes vertes doit être de 42 % et on fait un test sur 180 boîtes. La loi associée au nombre V de boîtes vertes est donc la loi binomiale de paramètres (180 ; 0,42).
En utilisant une feuille de tableur, on obtient la loi binomiale B(180 ; 0,42).
On observe que
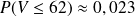 et
et
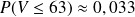 .
. Donc le plus petit entier a tel que
 % est a=63.
% est a=63.On observe que
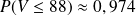 et
et
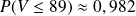 .
.Donc le plus petit entier b tel que
 % est b=89.
% est b=89.Ces deux valeurs correspondent à l'intervalle de fluctuation au seuil de 95 %.
L'échantillon comporte autant de boîtes bleues que de boîtes vertes, c'est-à-dire 90 de chaque.
90 n'étant pas compris entre 63 et 89, on peut penser que la machine est déréglée (au risque de 5%).
D'après les valeurs de a et b données dans la question précédente, on peut penser que la machine est déréglée si le nombre de boîtes vertes est inférieur à 63 ou supérieur à 89, c'est-à-dire si le nombre de boîtes bleues est inférieur à 91 (180-89) ou supérieur à 117 (180-63).
NB : on aurait trouvé les mêmes résultats en raisonnant sur le nombre de boîtes bleues avec la loi binomiale B(180 ; 0,58).