Activité d'approche
Simulation :
On sait pour une fonction \(f\) déterminer en un point d'abscisse \(a\) le nombre dérivé \(f'(a)\). Dès lors, on peut s'intéresser à la fonction \(f' : a\longmapsto f'(a)\) !
![]()
Reprenons l'activité du départ avec la fonction \(f(x)=x^2\). Affichons cette fois ci les cases Tangente, Pente Tangente pour connaître la valeur du nombre dérivé \(f'(a)\) et Nombre dérivée qui va afficher en vert la trace du point \(B(a ;f'(a))\).
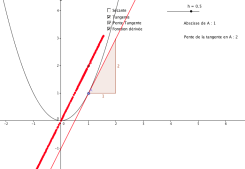
Activité d'introduction du nombre et de la fonction dérivée.
On peut alors constater en bougeant le point A que le nombre dérivé en \(a\) semble être \(2a\). La fonction dérivée de \(f(x)=x^2\) est la fonction linéaire \(f'(x)=2x\) représentée par trace du point B en vert.