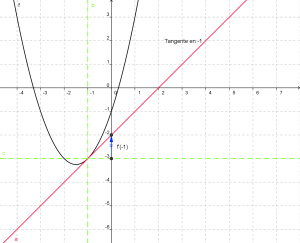
Déterminer l'équation de la tangente en un point
Soit la fonction \(f(x)=x^2+3x-1\)
On cherche l'équation réduite de la tangente au point d'abscisse \( a = -1\).
Question
A l'aide de la calculatrice, déterminer le nombre dérivé \(f'(-1)\).
Solution
Sur casio
Sur TI
Complément :
Par conséquent, on peut lire que \(f'(-1)=1\).
Question
En déduire l'équation réduite de la tangente au point d'abscisse \(-1\).
Indice
On se rappelle que celle-ci est donnée par la formule \(y=f'(a)(x-a)+f(a)\) .
Solution
Pour appliquer la formule, il nous manque encore \(f(-1)\) que nous allons calculer.
\(f(-1)=(-1)^2+3 \times (-1)-1 = 1-3-1=-3\)
Donc l'équation de la tangente est :
\(y=f'(-1)(x-(-1))+f(-1)=1(x+1)-3=x-2\)
Donc l'équation de la tangente en \(-1\) est \(y=x-2\).
On constate sur le graphe que la pente de la tangente est de 1 (flèche bleu), ce qui correspond au coefficient directeur de l'équation de cette tangente. L'ordonnée à l'origine (-2) permet de tracer la tangente facilement.
