Extremum
Rappel : Extremum
On se rappelle en seconde de la notion d'extremum d'une fonction.
Fondamental :
Soit \(f\) une fonction définie et dérivable sur un intervalle \(I\).
Si la dérivée \(f'\) s'annule en changeant de signe en \(c\in I\), alors \(f\) admet un extremum en \(c\).
Si f admet un extremum en \(c\in I\), alors \(f'(c)=0\).
Exemple :
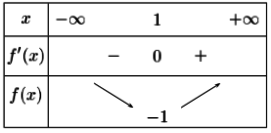
Le tableau de variation suivant montre que l'on a un extremum en 1, puisque la dérivée s'annule en 1 et change de signe.
Ici on a un minimum.
Attention :
Si la dérivée s'annule pour \(x=a\) sans changer de signe, alors f n'admet pas d'extremum.

On pourra considérer le contre exemple \(f(x)=x^3\) pour \(a=0\).