Etude de fonction
Soit \(f(x)=3x^2-6x+2\).
En étudiant le signe de la dérivée de cette fonction, nous allons retrouver les résultats que nous aurions pu trouver en utilisant ce que nous avons vu dans le chapitre sur l'étude du second degré concernant les variations des polynômes du second degré, mais de façon beaucoup plus rapide : nul besoin de trouver la forme canonique.
Question
Calculer la dérivée de \(f\) puis étudier le signe de \(f'\). En déduire le tableau de variation de la fonction \(f\).
Solution
Dérivée de f
\(f'(x)=6x-6\) car c'est la somme de 3 fonctions élémentaires que l'on sait dériver.
Signe de la dérivée
On étudie le signe de cette dérivée, en calculant \(6x-6 > 0\) (on se pose la question de savoir quand la dérivée est positive, on pourrait faire avec < donc négative).
Donc \(6x-6 > 0\) donne \(x > 1\) donc la dérivée est positive si \(x\) est plus grand que 1, inversement elle est négative si \(x\) est plus petit que 1.
Tableau de variations
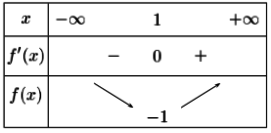
On fait apparaître dans le tableau :
L'ensemble de définition
Les valeurs de \(x\) remarquables (ici celle qui annule \(f'(x)\)) et les valeurs de \(f'\) et \(f\) pour ces valeurs.
Le signe de \(f'\)
Les variations de \(f\)