Définitions
On considère une fonction f définie sur un intervalle I, et un nombre réel \(a\) appartenant à I.
Définition : Maximum d'une fonction
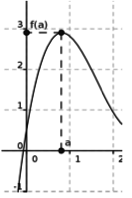
On dit que \(f(a)\) est un maximum de f sur l'intervalle I si pour tout réel x de I, on a \(f(x)\leq f(a)\).
Définition : Minimum d'une fonction
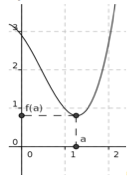
On dit que \(f(a)\) est un minimum de f sur l'intervalle I si pour tout réel x de I, on a \(f(x)\geq f(a)\).
Définition : Extremum d'une fonction
On dit qu'une fonction admet un extremum sur l'intervalle I lorsqu'elle admet un maximum ou un minimum sur cet intervalle.
Fondamental :
Lorsque sur un intervalle, une fonction change de sens de variation, elle admet un ou plusieurs extremums.