Utiliser le théorème du toit dans un tétraèdre
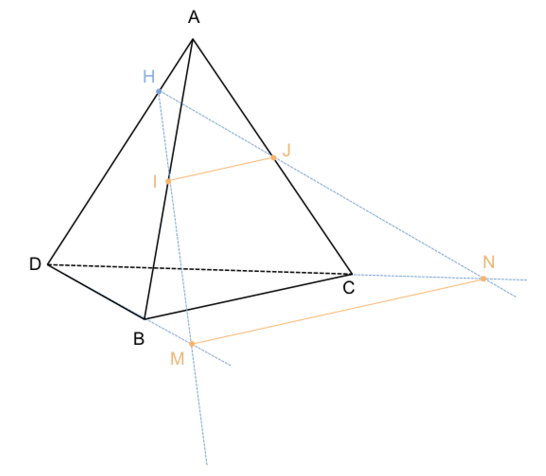
Soit un tétraèdre ABCD. On appelle I le milieu de [AB] et J le milieu de [AC].
Soit H un point du segment [AD] distinct de son milieu :
les droites (HI) et (DB) se coupent en M ;
les droites (HJ) et (DC) se coupent en N.
Question
Démontrer que la droite (IJ) est parallèle au plan (BCD)
Solution
Dans le triangle ABC, (IJ) est la droite des milieux des côtés [AB] et [AC].
On en déduit que (IJ) est parallèle à (BC).
Or, la droite (BC) est incluse dans le plan (BCD).
La droite (IJ) est ainsi parallèle à une droite du plan (BCD), elle est donc parallèle à ce plan.
Question
Démontrer que les droites (IJ) et (MN) sont parallèles.
Indice
On pourra utiliser le théorème du toit
Solution
On sait que :
La droite (IJ) appartient au plan (HMN)
La droite (BC) appartient au plan (DMN)
Les droites (IJ) et (BC) sont parallèles
Les plans (HMN) et (DMN) contiennent donc deux droites parallèles, (IJ) et (BC). D'après le théorème du toit, l'intersection de ces deux plans est alors parallèle à ces deux droites.
Or, les points M et N sont communs aux plans (HMN) et (DMN) : la droite (MN) est donc l'intersection de ces deux plans.
La droite (MN) est donc parallèle aux droites (IJ) et (BC).