Notation e
La relation fonctionnelle \(\exp (x+y)=\exp (x)\times \exp (y)\) n'est pas sans rappeler les propriétés sur les puissances : nous savons en effet depuis le collège que pour tout nombre \(a : a^{n+m}=a^m\times a^n\)
L'idée est donc de noter l'exponentielle comme une puissance en définissant un nouveau nombre fondamental en mathématique servant de base pour cette notation.
Définition : Le nombre d'Euler : le nombre e
On définit le nombre \(e=\exp(1)\).
On a alors \(\exp 2=\exp (1+1)=\exp 1\times \exp 1=e\times e=e^2\)
\(\exp 3=\exp (2+1)=\exp 2\times \exp 1=e^2 \times e=e^3\)
et en généralisant cette écriture \(\exp (x)=e^x\)
C'est la notation puissance de l'exponentielle.
Le nombre e s'appelle le nombre d'Euler. Nous en avons déterminé une valeur approchée au moyen de l'algorithme de la seconde activité de ce chapitre. Il faut retenir que \(e\approx 2,71828\).
On a bien sûr \(e^0=1\) et \(e^1=e\).
Fondamental : Relation fonctionnelle et conséquences immédiates
Pour tous réels x et y, et pour tout entier relatif n, on a les relations suivantes :
\(e^{x+y}=e^x\times e^y\)
\(e^{-x}=\frac{1}{e^x}\)
\(e^{x-y}=\frac{e^x}{e^y}\)
\(e^{nx}=\left(e^x\right)^n\)
Complément : Démonstration
Nous avons démontré la relation fonctionnelle donnant la première égalité.
\(e^{-x}\times e^x=e^{-x+x}=e^0=1\) d'où découle la seconde égalité.
\(e^{x-y}=e^x\times e^{-y}\) d'où découle la troisième égalité.
Démontrons la dernière égalité par récurrence :
Supposons que n est un entier naturel
Initialisation:pour \(n=0, e^{0x}=(e^x)^0=1\) donc la propriété est vraie pour \(n=0\).
Hérédité:Posons \(\mathcal P_n : e^{nx}=(e^x)^n\) pour tout x réel
Supposons que pour un certain k \(\mathcal P_k\) soit vraie.
\(e^{(k+1)x}=e^{kx+x}=e^{kx}\times e^x\)
D'après l'hypothèse de récurrence \(\mathcal P_k\) : \(e^{kx}=(e^x)^k\)
Donc \(e^{(k+1)x}=(e^x)^k\times e^x=(e^x)^{k+1}\).
Ce qui montre que \(\mathcal P_{k+1}\) est vraie. L'hypothèse de récurrence est donc héréditaire.
Conclusion:Le raisonnement par récurrence nous permet donc d'affirmer que pour tout entier naturel \(n\), \(e^{nx}=\left(e^x\right)^n\)
Si \(n\) est un entier relatif négatif, alors \(-n\) est un entier naturel et la démonstration ci-dessus s'applique en posant \(y=-x\).
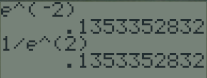
Exemple : A la calculatrice
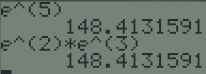
\(e^5=e^2\times e^3\)
\(e^{-2}=\frac{1}{e^2}\)
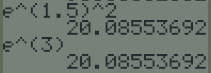
\((e^{1,5})^2=e^3\)