Théorème d'encadrement dit "des gendarmes"
Fondamental : Théorème d'encadrement (admis)
Soient trois suites \((v_n)\), \((u_n)\) et \((w_n)\) définies pour tout \(n\in \mathbb N\).
On suppose qu'à partir d'un certain rang, \(v_n\leqslant u_n\leqslant w_n\)
Si \((v_n)\) et \((w_n)\) tendent vers la même limite \(\ell\), alors la suite \((u_n)\) tend aussi vers \(\ell\)
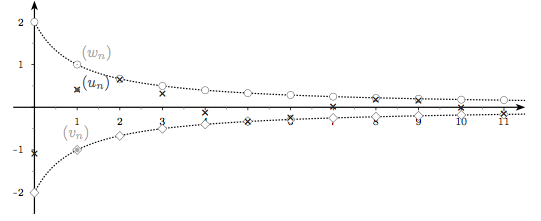
Exemple :
Soit \((u_n)\) la suite définie pour \(n\geqslant 1\) par \(u_n=\frac{\sin n}{n}\)
On peut encadrer facilement la suite \((u_n)\) par deux suites que l'on connaît bien :
Partant de l'inégalité pour tout \(n\) : \(-1\leqslant \sin n\leqslant 1\) et en divisant chaque membre par \(n\) (\(n\geqslant 1\)) :
On obtient :
\(-\frac{1}{n}\leqslant \sin n\leqslant \frac{1}{n}\)
Posons pour \(n\geqslant 1\) \(v_n=-\frac{1}{n}\) et \(w_n=\frac{1}{n}\)
On sait (ou on montre facilement) que \((v_n)\) et \((w_n)\) tendent vers 0
Le théorème des gendarmes nous permet d'affirmer que la suite \((u_n)\) est convergente et que sa limite est 0.