Exemples type
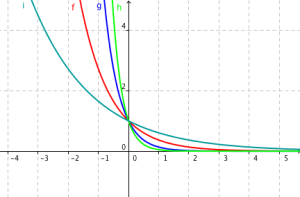
Exemple : fonctions de type exp(-kx) avec k>0
Soit k un réel strictement positif et \(f(x)=e^{-kx}\)
Alors \(f'(x)=-k.e^{-kx}\). L'exponentielle étant toujours positive et k positif, \(f'(x)\) est strictement négative pour tout réel x. La fonction f est donc strictement décroissante sur \(\mathbb{R}\).
De plus pour \(x=0\), \(f(x)=1\) quelque soit la valeur de k. On obtient donc les courbes pour différentes valeurs de k :
\(f(x)=e^{-x}\)
\(g(x)=e^{-2x}\)
\(h(x)=e^{-3x}\)
\(i(x)=e^{-x/2}\)
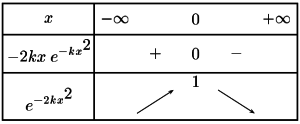
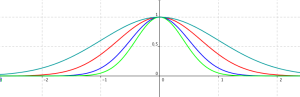
Exemple : fonctions de type exp(-kx^2) avec k>0
Soit k un réel strictement positif et \(g(x)=e^{-kx^2}\).
Alors \(g'(x)=-2kxe^{-kx^2}\). L'exponentielle étant toujours positive et k positif, \(g'(x)\) est du signe opposé à \(x\) pour tout réel \(x\). La fonction g est donc strictement croissante sur \(]-\infty ;0[\) et strictement décroissante sur \(]0 ;+\infty[\).
De plus pour \(x=0\), \(f(x)=1\) quelque soit la valeur de k. On obtient donc les courbes pour différentes valeurs de k :
\(f(x)=e^{-x^2}\)
\(g(x)=e^{-2x^2}\)
\(h(x)=e^{-3x^2}\)
\(i(x)=e^{-x^2/2}\)
On remarque cette forme particulière en cloche qui n'est pas sans rappeler la loi binomiale étudiée l'an dernier. Nous approfondirons cette question dans le chapitre sur la loi normale.