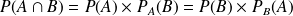Probabilités composées
On sait que si A et B sont deux événements, A étant possible,
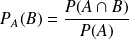. En multipliant cette égalité par
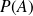non nul, on en déduit la formule suivante :
Fondamental :
Si l'on connaît la probabilité de l'événement A et la probabilité de l'événement B sachant que A est réalisé, la probabilité de l'événement
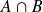est
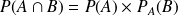
Exemple :
Un joueur de tennis réussit sa première balle de service à 75% et sa deuxième balle à 90%. Quelle est la probabilité qu'il commette une double faute ?
Si l'événement A est "le joueur rate sa première balle".
On sait d'après l'énoncé que
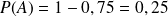.L'événement B est "Le joueur rate sa seconde balle"et l’événement
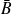est "Le joueur réussit sa deuxième balle".L'événement B sachant A est "le joueur rate sa seconde balle sachant qu'il a raté la première également".
On a d'après l'énoncé que
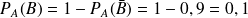
La double faute est l'événement
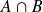. Or
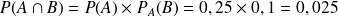
La probabilité que le joueur rate ses deux services est de 0,025.
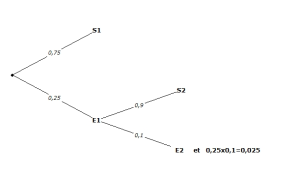
Visuellement cette situation se représente aisément à l'aide d'un arbre pondéré.
 |
On constate que la probabilité d'avoir une double faute correspond à la probabilité de la feuille E2. Celle-ci s'obtient d'après la formule précédente en faisant le produit des probabilités des branches menant à cette feuille. |
Remarque :
Si
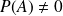et
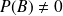, on a :
