Propriété fondamentale
Fondamental :
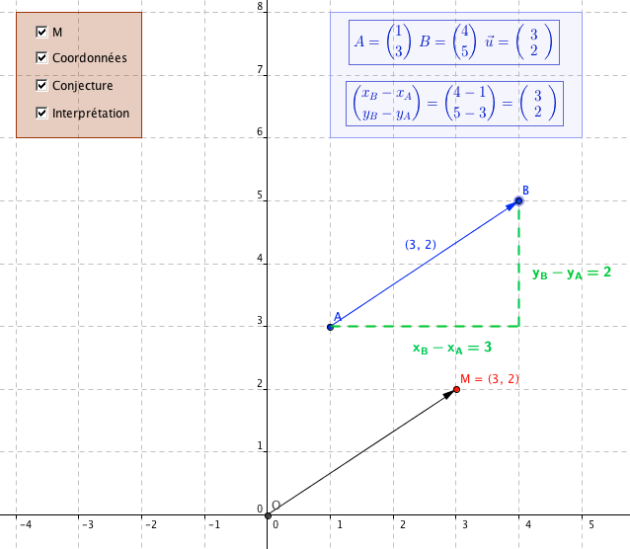
Dans un repère on considère les points \(A(x_A ;y_A)\) et \(B(x_B ;y_B)\).
Alors les coordonnées du vecteur \(\overrightarrow{AB}\) se calculent ainsi : \(\overrightarrow{AB} \left (\begin{array}{c}x_B-x_A\\y_B-y_A\end{array}\right )\).
Complément : Démonstration
En effet, on définit le point M tel que \(\overrightarrow{AB}\)=\(\overrightarrow{OM}\) dans le repère \((O,\overrightarrow{i},\overrightarrow{j})\).
[OB] et [AM] ont le même milieu K. D'après la formule du milieu on peut écrire :
d'une part \(x_K=\frac{x_B}{2}\) car K milieu de [OB],
d'autre part \(x_K=\frac{x_A+x_M}{2}\) car K milieu de [AM].
On obtient donc une équation (E) d'inconnue \(x_M\) : \(\frac{x_B}{2}=\frac{x_A+x_M}{2}\)
En multipliant par 2 de part et d'autre, on a \((E) \Leftrightarrow x_B=x_A+x_M\).
En retranchant \(x_A\), on a \((E) \leftrightarrow x_B-x_A=x_M\).
En procédant aux mêmes calculs sur les ordonnées on obtient de même \(y_M=y_B-y_A\), ce qui prouve le résultat énoncé.