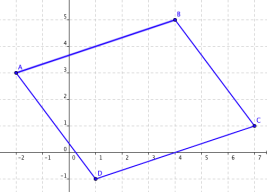
Dans un repère (O,I,J), on considère les points :
A(-2 ;3)
B(4 ;5)
C(7 ;1)
D(1 ;-1)
Question
Démontrer en utilisant les coordonnées de vecteurs que ABCD est un parallélogramme.
Indice
On pourra calculer les coordonnées de \(\overrightarrow{AB}\) et \(\overrightarrow{DC}\).
Solution
Coordonnées du 1er vecteur
Coordonnées du vecteur \(\overrightarrow{AB}\) :
4-(-2) =6
5-3=2
donc \(\overrightarrow{AB} \left (\begin{array}{c}6\\2\end{array}\right )\).
Coordonnées du 2ème vecteur
Coordonnées du vecteur \(\overrightarrow{DC}\) :
7-1=6
1-(-1)=2
donc \(\overrightarrow{DC} \left (\begin{array}{c}6\\2\end{array}\right )\).
Méthode :
Les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) ont les mêmes coordonnées donc ils sont égaux.
\(\overrightarrow{AB}\)=\(\overrightarrow{CD}\) donc ABDC est un parallélogramme.
Remarque : Alternative
On aurait pu également traiter l'exercice en montrant que \(\overrightarrow{AD}\) et \(\overrightarrow{BC}\) avaient comme coordonnées \(\left (\begin{array}{c}3\\-4\end{array}\right )\).
Remarque : Autre méthode
On aurait pu également résoudre l'exercice en montrant que les diagonales [AC] et [BD] avaient même milieu en calculant les coordonnées de ce milieu.