Vecteurs égaux
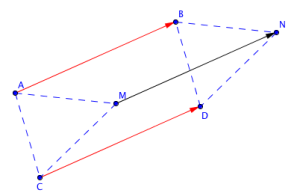
On note D le point associé à C par la translation de vecteur \(\overrightarrow{AB}\). Alors à tout point M, la translation de vecteur \(\overrightarrow{AB}\) et la translation de vecteur \(\overrightarrow{CD}\) associent le même point N.
En effet, si ABDC et ABNM sont des parallélogrammes, on montre qu'alors CDNM est aussi un parallélogramme. Cette propriété se démontre en utilisant le fait que si deux droites sont parallèles à une même troisième, alors elles sont parallèles entre elles, et que si un quadrilatère a deux côtés parallèles et de même longueur, alors c'est un parallélogramme.
Définition : Vecteurs égaux
Dire que les deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont égaux signifie que la translation qui transforme A en B transforme aussi C en D.
On note \(\overrightarrow{AB}=\overrightarrow{CD}\).
Fondamental :
Deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont égaux si et seulement si le quadrilatère ABDC est un parallélogramme, éventuellement aplati.
Attention : Attention à l'ordre des lettres
Notez l'inversion de l'ordre des lettres dans le parallélogramme :
\(\overrightarrow{AB}=\overrightarrow{CD} \Longleftrightarrow\) ABDC est un parallélogramme.
Fondamental :
Deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont égaux si et seulement si :
les droites (AB) et (CD) sont parallèles,
On va de A vers B et de C vers D en se déplaçant dans le même sens,
les longueurs AB et CD sont égales.
On dit que les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) ont la même direction, le même sens et la même longueur.