Utiliser les vecteurs pour démontrer
A,B,O,O' sont 4 points distincts.
C et D sont symétriques respectifs de A et B par rapport à O.
E et F sont symétriques respectifs de A et B par rapport à O'.
Question
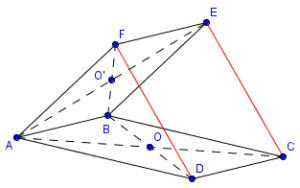
Démontrer que DCEF est un parallélogramme.
Indice
Exploiter les symétriques pour mettre en évidence des parallélogrammes et donc des égalités de vecteurs.
Indice
Montrer que \(\overrightarrow{AB}=\overrightarrow{DC}\) et que \(\overrightarrow{AB}=\overrightarrow{FE}\).
Solution
On sait que [AC] et [BD] se coupent en leur milieu (O) donc ABCD est un parallélogramme.
De là, on en déduit que \(\overrightarrow{AB}=\overrightarrow{DC}\).
On sait que [AE] et [BF] se coupent en leur milieu (O') donc ABEF est un parallélogramme.
De là, on en déduit que \(\overrightarrow{AB}=\overrightarrow{FE}\).
Les vecteurs \(\overrightarrow{DC}\) et \(\overrightarrow{FE}\) sont donc deux représentants du vecteur \(\overrightarrow{AB}\). Ils sont donc égaux.
Puisque \(\overrightarrow{DC}\) =\(\overrightarrow{FE}\), alors on conclut que DCEF est un parallélogramme.
Remarque :
Pour résoudre cet exercice, nous avons utilisé la propriété vue ici à la fois dans le sens direct et dans le sens réciproque. Il est donc important de bien connaître la signification de l'équivalence (si et seulement si).