Quelques exemples d'expériences aléatoires
Roue de couleurs
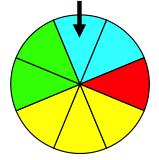
On fait tourner une roue marquée sur ses secteurs de couleurs différentes et on regarde la couleur du secteur marqué par la flèche.
Question
Quel est l'univers associé à cette expérience ?
Combien possède t-il d'issues ?
Solution
Ω={ bleu ; vert ; jaune ; rouge }
Question
Citer deux événements non élémentaires.
Citer un événement élémentaire.
Citer un événement impossible.
On écrira chacune des réponses sous forme d'une description par une phrase puis sous forme d'un ensemble.
Solution
Deux événements non élémentaires
A : « Obtenir la couleur bleue ou la couleur rouge »
A= { bleu ; rouge }
B : « ne pas obtenir la couleur verte »
B= { bleu ; jaune : rouge }
Un événement élémentaire
C : « obtenir la couleur verte »
c={vert}
Un événement impossible
D : « obtenir la couleur orange »
D=Ø
Jeu de Pile ou Face
On lance deux fois une pièce de monnaie et on note à chaque fois la face « Pile »
ou « Face »
obtenue
Question
Quel est l'univers associé à cette expérience ?
Combien possède t-il d'issues ?
Solution
Ω={ (P,P) ; (P,F) ; (F,P) ; (F,F) }
L'expérience possède 4 issues possibles.
Question
Citer deux événements non élémentaires.
Citer un événement élémentaire.
Citer un événement impossible.
On écrira chacune des réponses sous forme d'une description par une phrase puis sous forme d'un ensemble.
Solution
Deux événements non élémentaires
A : « Obtenir exactement une fois Pile »
A= { (P,F) ; (F ;P) }
B : « obtenir au moins une fois Pile »
B={ (P,F) ; (F ;P) ; (P ;P) }
Un événement élémentaire
C : « ne pas obtenir Pile »
c={ (F,F) }
Un événement impossible
D : « obtenir trois fois Pile »
D=Ø
Jeu avec deux dés
On lance deux fois un dé à 6 faces bien équilibré et on note le numéro de chaque face obtenue.
Question
Quel est l'univers associé à cette expérience ?
Combien possède t-il d'issues ?
Solution
Ω={ (1,1) ; (1,2) ; (1,3) ; ... ; (1,6) ... ; (2,1) ; ... ; (2,6) ; ... (6,1) ; ... ; (6,6)}
L'expérience possède \(6\times 6=36\) issues possibles.
Question
On considère les événements
A : « La somme des deux faces est 5 »
B : « La somme des deux faces est égale au produit des deux faces »
Écrire chacun de ces événements sous forme d'ensembles.
Combien A et B possèdent-ils d'issues ?
Solution
A={ (1,4) ; (2,3) ; (3,2) ; (4,1) }
A possède 4 issues.
B={(2,2)}
B est un événement élémentaire.