Mise en situation : signe d'une fonction affine
Une entreprise réalise en 2010 un bénéfice net de 6000 €. En 2013, ce bénéfice n'est plus que de 4000 €.
En supposant que la situation évolue de manière régulière comme entre 2010 et 2013, que peut-on prédire sur l'avenir de cette entreprise ?
Question
Pourquoi peut-on représenter cette situation à l'aide d'une fonction affine ?
En supposant que \(x\) compte le nombre d'années écoulées depuis 2010 et que l'on exprime le bénéfice de l'entreprise en milliers d'euros, donner l'expression de \(f(x)\) correspondant à cette situation.
Solution
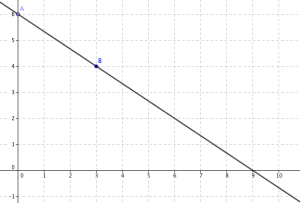
On nous dit que la baisse se fait de manière régulière. On peut donc la représenter sur un graphique à l'aide d'une droite.
Cette droite est caractéristique d'une fonction affine.
Méthode : Déterminer l'expression d'une fonction affine à partir de deux points
On sait par l'énoncé que : \(f(0)=6\) et \(f(3)=4\)
De la première valeur on déduit que \(b=6\)
On sait de plus que \(a=\dfrac{f(3)-f(0)}{3-0}=\frac{4-6}{3}=-\dfrac{2}{3}\)
Donc \(f(x)=-\frac{2}{3}x+6\)
Question
Quel est le sens de variation de \(f\) ? que peut-on en déduire pour l'entreprise ?
Solution
Le coefficient directeur \(a=-\dfrac{2}{3}\) est négatif donc la fonction \(f\) donnant le bénéfice est décroissante.
Le bénéfice de l'entreprise est donc en baisse d'année en année. L'entreprise va finir par réaliser des pertes.
Question
A partir de quelle année l'entreprise va t-elle réaliser des pertes ?
Solution
L'entreprise réalisera des pertes lorsque l'on aura \(f(x)<0\). Résolvons donc cette inéquation :
\(-\frac{2}{3}x+6<0 \Longleftrightarrow -\frac{2}{3}x<-6 \Longleftrightarrow x>6\times \dfrac{3}{2}\)
Donc
si \(x>9\) on a \(f(x)<0\)
si \(x=9\) on a \(f(x)=0\)
si \(x<9\) on a \(f(x)>0\)
On peut résumer cela dans le tableau de signe suivant :
x | 9 | ||
|---|---|---|---|
f(x) | + | 0 | - |
A partir de 2019, l'entreprise va réaliser des pertes.