La Fonction carré
Définition : Fonction carré
La fonction définie sur \(\mathrm{R}\), qui à tout nombre réel \(x\) associe son carré \(x^2\), est appelée fonction carré.
Fondamental : Propriété 1
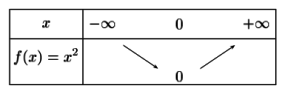
La fonction \(f :x \longmapsto x^2\) est :
décroissante sur l'intervalle \(]-\infty ;0]\)
croissante sur l'intervalle \([0 ;+\infty[\)
Complément : Démonstration
Montrons que la fonction carré est croissante sur \([0,+\infty[\).
Soient \(u\) et \(v\) deux réels positifs tels que \(u>v>0\).
\(f(u)-f(v)=u^2-v^2=(u+v)(u-v)\)
Or \(u+v>0\) et \(u-v>0\) car \(u>v>0\).
Donc \(f(u)-f(v)>0\) et alors \(f(u)>f(v)\).
Pour tous nombres réels positifs \(u\) et \(v\) tels que \(u>v\) on a \(f(u)>f(v)\) donc la fonction \(f\) est croissante sur \([0,+\infty[\)
Montrons que la fonction carré est décroissante sur \(]-\infty ;0]\).
Soient \(u\) et \(v\) deux réels négatifs tels que \(u<v<0\).
\(f(u)-f(v)=u^2-v^2=(u+v)(u-v)\)
Or \(u+v<0\) et \(u-v<0\) car \(u<v<0\),
donc \(f(u)-f(v)>0\) et alors \(f(u)>f(v)\).
Pour tous nombres réels négatifs \(u\) et \(v\) tels que \(u<v\) on a \(f(u)>f(v)\) donc la fonction \(f\) est décroissante sur \(]-\infty ;0]\).
Définition : Représentation graphique
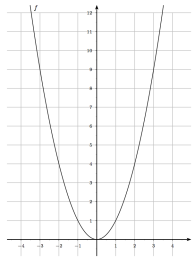
Dans un repère orthogonal d'origine O, la représentation graphique de la fonction carré est appelée parabole de sommet O.
Fondamental : Propriété 2
Dans un repère orthogonal, la parabole Ρ représentant la fonction carré est symétrique par rapport à l'axe des ordonnées.
Complément : Démonstration
Pour tout nombre réel \(x\), le point \(M(x ;x^2)\) appartient à la parabole Ρ.
Le symétrique de \(M\) par rapport à l'axe des ordonnées est le point \(M'(-x ;x^2)\).
Or \((-x)^2=x^2\) donc le point \(M'\) appartient aussi à la parabole Ρ.