Activité d'approche
Aire d'une couronne
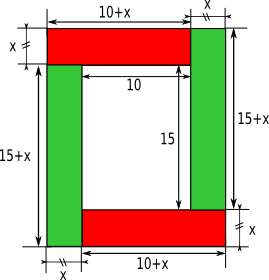
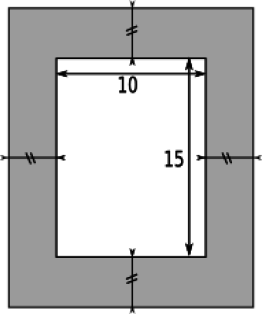
La figure ci-dessous est constituée de deux rectangles.
Ces deux rectangles forment une couronne (partie grisée).
Elle a la même largeur sur les quatre côtés.
Sachant que l'aire de la couronne est égale à l'aire du rectangle intérieur (en blanc), quelle est la largeur de cette couronne ?
Question
Question
Écrire une équation exprimant que l'aire de la couronne est égale à l'aire du rectangle intérieur. Sait-on la résoudre ? Pourquoi ?
Solution
Mise en équation
L'aire de la couronne est égale à l'aire du rectangle intérieur :
\(4x^2+50x=10 \times 15\)
\(4x^2=-50x+150\)
\(x^2=-12,5x+37,5\)
Remarque :
Cette équation est une équation faisant intervenir l'inconnue au carré. Nous n'avons pas les outils en seconde pour résoudre ce type d'équation sous forme algébrique. Nous devrons nous rabattre sur une résolution graphique du problème, l'étude des fonctions dans les chapitres précédents nous ayant fourni les outils nécessaires.
Question
Tracer dans un repère les fonctions
\(f(x)=x^2\)
\(g(x)=-12,5x+37,5\)
Lire graphiquement les solutions de l'équation \(f(x)=g(x)\).
En déduire la solution au problème posé.
Indice
On pourra s'aider de la calculatrice pour obtenir l'allure de la courbe représentative de la fonction carré.
Solution
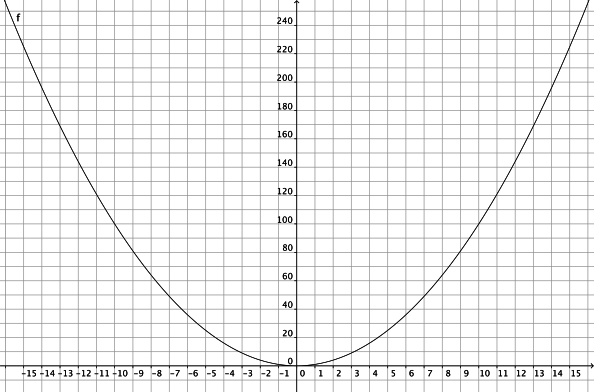
On superpose au graphique de la fonction carré le tracé de la droite d'équation \(y=12,5x+37,5\) dont l'étude a été réalisée au chapitre précédent.
L'intersection des deux courbes donne graphiquement les solutions de l'équation f(x)=g(x). Pour en déduire les solutions éventuelles au problème posé, on se souvient que le nombre cherché est une longueur. On ne va donc s'intéresser qu'à la solution positive, donc 2,5. C'est, à priori, une valeur approchée de la solution.
La largeur de la couronne recherchée est donc 2,5 cm environ.