Propriétés générales
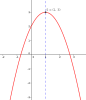
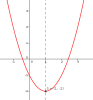
La simulation précédente nous donne une idée très précise du comportement des fonctions polynôme du second degré. On s'aperçoit qu'elles partagent toutes des propriétés déjà étudiées avec la fonction carré. Les propriétés principales que nous allons voir ci-dessous seront admises cette année dans le cas général.
Fondamental : Variation des polynômes du second degré
Soit f une fonction polynôme du second degré. Alors son tableau de variation est :
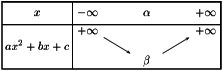ou 
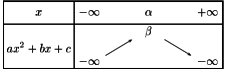
En particulier, le sens de variation change pour une certaine valeur de \(x=\alpha\). Une fonction polynôme du second degré admet dont un minimum ou un maximum selon les cas qui est atteint en \(x=\alpha\)
Les propriétés vues sur la parabole représentant la fonction carré se généralisent également :
Fondamental : Parabole et axe de symétrie
Dans un repère orthonormé, la courbe représentative d'une fonction polynôme du second degré est une parabole de sommet \(S (\alpha,\beta)\). Cette parabole admet un axe vertical de symétrie dont l'équation est \(x=\alpha\)
ou 