Forme canonique d'un polynôme du second degré
Soit f la fonction définie sur \(\mathbb{R}\) par \(f(x)=2+(x-3)^2\).
Question
Justifier que f est une fonction polynôme du second degré.
Solution
En développant l'expression de f, on obtient \(f(x)=2+x^2-6x+9=x²+6x+11\).
La fonction f est bien de la forme \(ax^2+bx+c\) avec \(a=1\) ; \(b=-6\) et \(c=11\).
Question
Justifier que f admet un extremum que l'on précisera par le calcul.
Indice
Utiliser le fait qu'un carré est toujours positif dans l'expression du départ.
On pourra s'aider de la calculatrice ou le logiciel geogebra pour se faire une idée (conjecturer) du résultat.
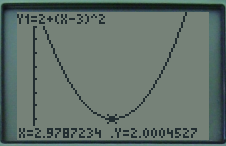
Solution
D'après la propriété du cours, on sait que f admet un extremum. C'est soit un minimum soit un maximum selon la famille à laquelle la courbe appartient.
On peut facilement savoir qu'il s'agit d'un minimum : en calculant \(f(2)\), \(f(3)\) et \(f(4)\), on obtient :
\(f(2)=2+(2-3)²=3\), \(f(3)=2\), et \(f(4)=2+(4-3)²=2+1²=3\). La fonction est donc d'abord décroissante, puis croissante. Elle admet donc un minimum.
Reprenons l'expression de f au départ : \(f(x)=2+(x-3)^2\). On sait qu'un carré est toujours positif donc pour tout x réel, \((x-3)^2\geq0\)
En ajoutant 2 de part et d'autre de l'inégalité, \(2+(x-3)^2\geq2\) donc \(f(x)\geq2\) pour tout réel x.
De plus \(f(3)=(3-3)^2+2=2\).
Conclusion : la fonction f admet comme minimum 2. Il est atteint en \(x=3\).
On peut utiliser un autre moyen pour démontrer à partir des valeurs obtenues précédemment, on a constaté que f(2)=f(4).
La courbe étant symétrique, l'axe de symétrie est donc forcément la droite d'équation \(x=\frac{2+4}{2} donc x=3\), Donc, le sommet a pour abscisse 3. En calculant \(f(3)\), on trouve la valeur du minimum.
La forme \(f(x)=a(x-\alpha)^2+\beta\) se révèle pratique pour trouver le sommet de la parabole. Cette forme est appelée forme canonique du polynôme \(f(x)\).
Sur la figure ci-dessous, déplacer les curseurs \(a\), \(\alpha\) et \(\beta\) pour constater leur effet sur la position de la courbe par rapport à l'axe des abscisses et son orientation.
Résumé :
Le nombre \(\alpha\) donne l'abscisse du sommet S de la parabole.
Les coordonnées du sommet sont donc \(S(\alpha ;f(\alpha))\), c'est-à-dire \(S(\alpha,\beta)\).
Le signe du nombre \(a\) indique si la parabole est orientée "vers le haut, ou "vers le bas" : si \(a>0\), alors elle est tournée vers le haut, et vers le bas si \(a\) est négatif.
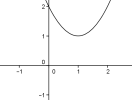
Si \(a>0\) et \(\beta>0\), la parabole ne coupe pas l'axe des abscisses :
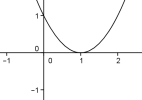
Si \(a>0\) et \(\beta=0\), la parabole est tangente à l'axe des abscisses :
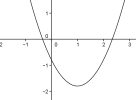
Si \(a>0\) et \(\beta<0\), la parabole coupe l'axe des abscisses en 2 points :
Si \(a<0\) et \(\beta>0\), la parabole coupe l'axe des abscisses en 2 points.
Si \(a<0\) et \(\beta=0\), la parabole est tangente à l'axe des abscisses.
Si \(a<0\) et \(\beta<0\), la parabole ne coupe pas l'axe des abscisses.