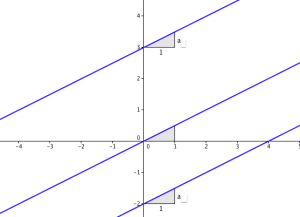
Droites parallèles
On considère dans un repère deux droites \((d)\) et \((d')\) d'équations respectives \((d) : y=ax+b\) et \((d') : y=a'x+b'\).
Le coefficient directeur a s'interprète géométriquement comme le déplacement vertical effectué sur la droite lors d'un déplacement horizontal de 1. Le vecteur de coordonnées (1 ;a) donne donc la direction de la droite (d).
De la même manière, le vecteur de coordonnées (1 ;a') donne la direction de la droite (d').
Or ces vecteurs sont colinéaires si et seulement si a=a' (règle du produit en croix : 1\times a'=1\times a).
Par conséquent, on peut énoncer la propriété suivante :
Fondamental :
Dans un repère, deux droites non parallèles à l'axe des ordonnées sont parallèles si et seulement si elles ont le même coefficient directeur.
Complément :
Par conséquent, on peut également affirmer que deux droites non parallèles à l'axe des ordonnées sont sécantes si et seulement si elles n'ont pas le même coefficient directeur.