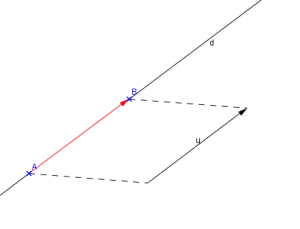
Vecteur directeur d'une droite
Définition :
On appelle vecteur directeur d'une droite d n'importe quel vecteur non nul \(\overrightarrow{u}\) dont la direction est celle de d.
Fondamental :
Soient \( \overrightarrow{u}\) et \(\overrightarrow{v}\) des vecteurs directeurs de deux droites d et d'.
Les deux droites d et d' sont parallèles si et seulement si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires.
Fondamental :
La droite \(d\) passant par un point A et de vecteur directeur \(\overrightarrow{u}\) est l'ensemble des points M tels que \(\overrightarrow{u}\) et \(\overrightarrow{AM}\) sont colinéaires.
Vecteur directeur de droite