Intervalle de fluctuation et loi binomiale
Avec les notations introduites au début du paragraphe, le nombre d'individus possédant le caractère étudié
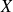 suit la loi binomiale
suit la loi binomiale
 .
.
 | On va diviser l'ensemble {0 ;1 ;2 ;... ;n} des valeurs possibles de
|
Fondamental : Propriété admise
Avec les notations précédentes, on définit :
 est le plus petit entier tel que
est le plus petit entier tel que
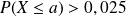
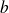 est le plus petit entier tel que
est le plus petit entier tel que
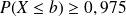
On a alors
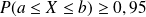 .
.
La fréquence
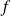 d'apparition du caractère dans l'échantillon étant égale à
d'apparition du caractère dans l'échantillon étant égale à
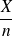 , on se ramène à l'intervalle [0 ;1] en divisant par n. Ainsi
, on se ramène à l'intervalle [0 ;1] en divisant par n. Ainsi
 .
.
Définition :
L'intervalle
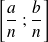 est appelé intervalle de fluctuation au seuil de 95%.
est appelé intervalle de fluctuation au seuil de 95%.
Exemple :
Reprenons l'exemple du paragraphe précédent avec la loi
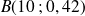 . Pour déterminer l'intervalle de fluctuation avec la méthode énoncée ci-dessus, il est très pratique d'utiliser la loi binomiale cumulée.
. Pour déterminer l'intervalle de fluctuation avec la méthode énoncée ci-dessus, il est très pratique d'utiliser la loi binomiale cumulée.
k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,0004 | 0,035 | 0,137 | 0,334 | 0,582 | 0,798 | 0,929 | 0,983 | 0,998 | 1 | 1 |
Les deux colonnes mises en évidence dans le tableau de la binomiale cumulée correspondent au dépassement des deux seuils de 0,025 (2,5%) et 0,975 (97,5%). On lit alors que :
le plus petit entier
 tel que
tel que
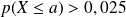 est
est
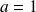 ,
,le plus petit entier
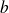 tel que
tel que
 est
est
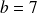 .
.
On peut en guise de vérification (mais ce n'est pas nécessaire dans les exercices) calculer :
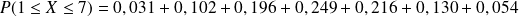 ,
,
donc
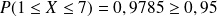 , ce qui est conforme à ce qui est annoncé dans la propriété du cours.
, ce qui est conforme à ce qui est annoncé dans la propriété du cours.
L'intervalle de fluctuation s'obtient en divisant les bornes
 et
et
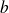 par
par
 , ici 10. L'intervalle de fluctuation est donc
, ici 10. L'intervalle de fluctuation est donc
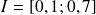 .
.
Complément :
Pour information, en utilisant la formule vue en seconde de l'intervalle de fluctuation :
donc
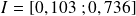 .
.
La méthode vue en seconde a l'avantage d'être plus simple à mettre en œuvre mais donne ici un résultat moins précis. On est en effet ici en dehors des conditions d'application[1] de la formule car la taille de l'échantillon (10) est insuffisante. La formule d'approximation de seconde fonctionne bien lorsque
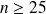 .
.