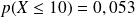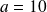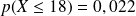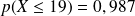Intervalle fluctuation
Dans un sac contenant des bulbes de tulipe, 60% d'entre eux donneront des tulipes blanches. On prélève un échantillon de 24 bulbes.
Question
On note
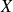la variable aléatoire désignant le nombre de bulbes qui donneront des tulipes blanches. Quelle est la loi de probabilité de
?
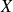Le nombre
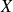de bulbes de tulipes blanches dans cet échantillon suit la loi binomiale de paramètres n=24 et p=0,6.
Question
A l'aide de la calculatrice ou du tableur, compléter le tableau suivant en arrondissant les valeurs au millième
k | 8 | 9 | 10 | 11 | 12 | ... | 17 | 18 | 19 | 20 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|
p(X=k) | ... | ... | |||||||||
p(X≤k) | ... | ... |
A l'aide du tableur, on pourra réaliser un tableau semblable à ceci :
La formule figurant dans la cellule
B2est=LOI.BINOMIALE(B1;24;0,6;0)La formule figurant dans la cellule
B3est=LOI.BINOMIALE(B1;24;0,6;1)
Le dernier paramètre (0 ou 1) indique si la loi est non cumulée ou cumulée.
Pour savoir comment procéder à la calculatrice, référez-vous aux vidéos proposées ci-dessous.
En tirant la formule vers la droite sur le tableur, on peut ainsi compléter le tableau.
k | 8 | 9 | 10 | 11 | 12 | ... | 17 | 18 | 19 | 20 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|
p(X=k) | 0,005 | 0,014 | 0,032 | 0,061 | 0,09 | ... | 0,096 | 0,056 | 0,027 | 0,010 | ... |
| 0,008 | 0,022 | 0,053 | 0,114 | 0,213 | ... | 0,904 | 0,960 | 0,987 | 0,996 | ... |
Question
En déduire l'intervalle de fluctuation au seuil de 95%
Observer dans le tableau obtenu ci-dessus les valeurs a et b de k pour lesquelles les seuils de 0,025 et 0,975 sont dépassés.
Dans un échantillon de 24 bulbes, il y a donc entre 10 et 19 bulbes de tulipe blanche avec une probabilité d'au moins 95%. L'intervalle de fluctuation au seuil de 95% est donc
|  |
