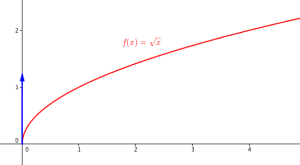
Dérivée de la fonction racine
Fondamental :
La fonction \(f : x \longmapsto \sqrt{x}\) est définie sur \([0 ;+\infty[\)
\(f\) est dérivable sur \(]0 ;+\infty[\) et \(f'(x)=\frac{1}{2\sqrt{x}}\) si \(x>0\).
Remarque :
On fera attention au fait que l'intervalle de définition de \(f\) n'est pas le même que celui sur lequel \(f\) est dérivable. En effet, la fonction racine n'est pas dérivable en 0.
Géométriquement, on peut interpréter ce phénomène en remarquant que la tangente en 0 à la courbe est verticale. Celle-ci n'a donc pas de pente et n'a pas d'équation réduite de la forme \(y=ax+b\).