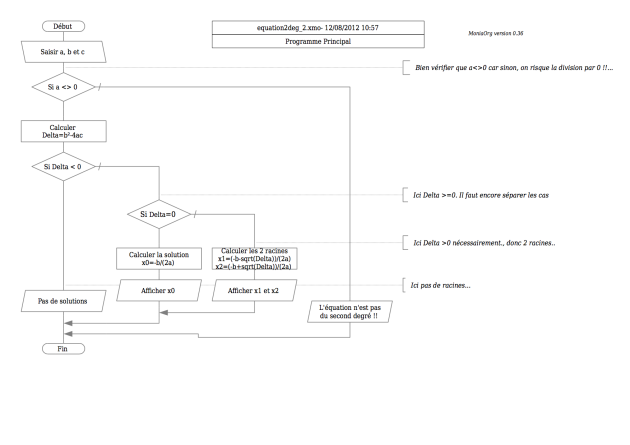
Algorithme de résolution d'une équation du second degré
Question
Question
Écrire un programme en Python (v 2.7) implémentant cet algorithme.
Indice
On pourra commencer son programme par les lignes d'entêtes suivantes :
# -*- coding: latin1 -*-
from __future__ import division
from math import sqrt
La première permet la gestion correcte de l'affichage des accents.
La seconde permet un comportement "normal" de la division.
La troisième permet d'utiliser la fonction sqrt : racine carrée.
Ces trois lignes peuvent être systématiquement ajoutées dans tout programme python que nous ferons cette année.
Indice
La saisie des données dans une variable peut se faire au moyen de l'instruction
a=input("Saisir la valeur de a : ")
L'affichage d'un message se fait au moyen de l'instruction print "La valeur de a est : ", a
Indice
L'enchaînement des tests peut être effectué au moyen de l'instruction elif condition: équivalente à else if condition :
Solution
Syntaxe : code en python 2.7 :
# -*- coding: latin1 -*-
from __future__ import division
from math import sqrt
a=input("entrer a")b=input("entrer b")c=input("entrer c")if a<>0:
Delta=b*b-4*a*c
if Delta < 0:
print "Il n'y a pas de solution."
elif Delta==0:
x0=-b/(2*a)
print "L'unique solution est : ",x0
else:
x1=(-b-sqrt(Delta))/(2*a)
x2=(-b+sqrt(Delta))/(2*a)
print "Il y a deux solutions qui valent environ ",x1, " et ", x2, "."
else:
print "Ce n'est pas un trinôme du second degré"