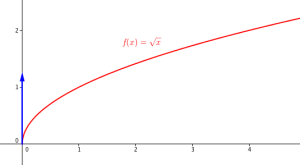
Dérivée de la fonction racine
Fondamental :
La fonction \(f : x \longmapsto \sqrt{x}\) est définie sur \([0 ;+\infty[\)
f est dérivable sur \(]0 ;+\infty[\) et \(f'(x)=\frac{1}{2\sqrt{x}}\)
Remarque :
On fera attention au fait que l'intervalle de définition de f n'est pas le même que celui sur lequel f est dérivable. En effet, la fonction racine n'est pas dérivable en 0.
Géométriquement, on peut interpréter ce phénomène en remarquant que la tangente en 0 à la courbe est verticale. Celle-ci n'a donc pas de pente et n'a pas d'équation réduite de la forme \(y=ax+b\).