Algorithme de dichotomie
On considère la fonction \(f :x\longmapsto x^3+x^2-x+1\) définie sur l'intervalle [-2 ;2]
Question
Dresser le tableau de variations de f
Solution
Calcul de la dérivée
\(f'(x)=3x^2+2x-1\)
Résolution de l'équation f'(x)=0
Cherchons les racines du polynôme \(3x^2+2x-1\) :
\(\Delta=4+12=16\)
\(x_1=\frac{-2-\sqrt{16}}{6}=-1\)
\(x_2=\frac{-2+\sqrt{16}}{6}=\frac{1}{3}\)
Le coefficient dominant est positif donc f' est positive en dehors des racines
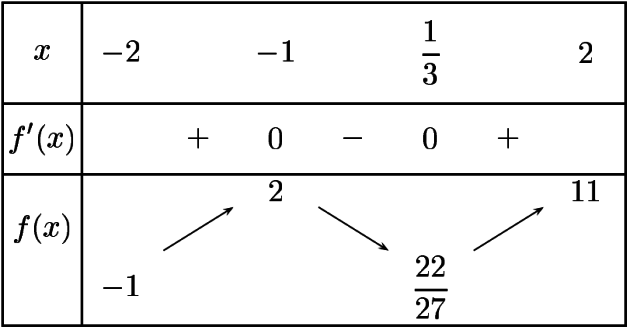
Tableau de variations
On calcule les valeurs de la fonction
\(f(-2)=-1\)
\(f(-1)=2\)
\(f\left(\frac{1}{3}\right)=\frac{22}{27}\)
\(f(2)=11\)
On en déduit le tableau de variations suivant :
Question
Déterminer les valeurs du réel \(k\) pour que l'équation \(f(x)=k\) admette au moins une solution.
Solution
Sur [-2 ;2], le tableau de variations montre que le minimum de la fonction est -1 et le maximum est 11.
De plus la fonction f est un polynôme donc continue sur \(\mathbb R\).
Donc pour tout réel \(k\in[-1 ;11]\), d'après le TVI, l'équation \(f(x)=k\) admet au moins une solution.
On cherche à résoudre l'équation \(f(x)=0\) . On considère l'algorithme suivant :
A prend la valeur -2
B prend la valeur -1
M prend la valeur -1,5
P=0,1
Tant Que B-A>P
... Si f(M)*f(A)>0
... ... A prend la valeur M
... Sinon
... ... B prend la valeur M
... M prend la valeur (A+B)/2
Fin TantQue
Afficher M
Question
Compléter le tableau suivant en donnant à chaque début de passage dans la boucle les valeurs demandées.
En déduire la valeur retournée par l'algorithme.
Etape 1 | Etape 2 | Etape 3 | Etape 4 | Etape 5 | |
|---|---|---|---|---|---|
A | -2 | ||||
B | -1 | ||||
M | -1,5 | ||||
f(A) | -1 | ||||
f(M) | 1,375 | ||||
B-A | 1 |
Solution
Etape 1 | Etape 2 | Etape 3 | Etape 4 | Etape 5 | |
|---|---|---|---|---|---|
A | -2 | -2 | -2 | -1,875 | -1,875 |
B | -1 | -1,5 | -1,75 | -1,75 | -1,8125 |
M | -1,5 | -1,75 | -1,875 | -1.8125 | -1.84375 |
f(A) | -1 | -1 | -1 | -0,2 | |
f(M) | 1,375 | 0,45 | -0,2 | 0,14 | |
B-A | 1 | 0,5 | 0,25 | 0,125 | 0,0625 |
A l'étape 5, B-A est inférieur à la précision de 0,1 demandée donc on sort de la boucle.
La valeur affichée par l'algorithme est la valeur de M donc -1,84375.
Question
Expliquer le rôle de cet algorithme et son fonctionnement.
Solution
Cet algorithme sert à déterminer une valeur approchée à la précision P de la solution de l'équation \(f(x)=0\) situé dans un intervalle [A ;B]
On commence par initialiser les bornes de l'intervalle de recherche : Ici on recherche la solution dans l'intervalle [-2 ;-1]. L'existence d'une solution unique dans cet intervalle nous est donnée par le tableau de variation calculé à la première question.
La méthode consiste ensuite à diviser à chaque étape par deux la longueur de l'intervalle en calculant dans la variable M le centre de ce dernier.
On réitère le procédé en prenant pour intervalle de recherche :
[M ;B] si f(A) et f(M) sont de même signe (ce qui nous dit que la solution cherchée n'est pas dans [A ;M]),
[A ;M ] si f(A) et f(M) sont de signe contraire (ce qui nous dit que la solution cherchée est dans [A ;M]).
La boucle s’arrête lorsque l'intervalle de recherche a une longueur inférieure à la précision P recherchée.
Cet algorithme met en œuvre la méthode dite de dichotomie qui consiste à diviser par deux la longueur de recherche en prenant le milieu de l'intervalle à chaque fois.
Chacun a, peut-être sans le savoir, déjà utilisé cet algorithme dans des jeux type "trouver le nombre entre 0 et 100 auquel je pense". On essaye 50, et si la personne répond plus petit, on essaye 25 et ainsi de suite jusqu'à trouver le nombre cherché.
Question
Programmer cet algorithme et l'adapter pour donner une valeur approchée de la solution \(f(x)=0\) à 0,0001 près.
Indice
On pourra utiliser Python en ligne par exemple ou la calculatrice.
Solution
Version Python
La valeur retournée est -1.83926 qui est une valeur approchée de la solution de l'équation f(x)=0 à \(10^{-4}\) près.
Solution
Sur calculatrice Casio
On programme la fonction dans Y1 comme pour faire une table de valeur pour plus de commodité dans l'écriture du programme.

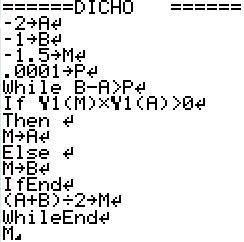
Voici le programme pour Casio.
La difficulté dans la saisie de ce programme est l'accès à la fonction Y1. Celui-ci se fait via le menu \(\fbox{VARS}\) - \(\fbox{GRPH}\) (F4) qui affiche le menu suivant :![]()
Le Y1 se fait alors par la touche \(\fbox{F1}\) suivie de \(\fbox{1}\)
Complément : Sur calculatrice TI
Le programme est pratiquement identique. Vous l'adapterez sans difficulté, sauf pour l'accès à la fonction Y1...
Comme pour Casio, on stocke la fonction dans la liste des fonctions comme pour un tableau de valeur.

L'accès à Y1 depuis l'éditeur de programme se fait par la touche \(\fbox{VAR}\) puis onglet Y-VARS premier choix puis sélectionner la fonction.