TVI et limites infinies
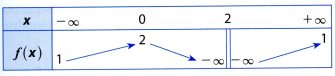
Soit la fonction \(f\) dont le tableau de variations est donné ci-dessous.
Question
Démontrer que l'équation \(f(x)=0\) admet exactement deux solutions dans \(\mathbb R \backslash \{2\}\)
Solution
Sur l'intervalle \(]-\infty ;0]\), d'après le tableau de variations, \(f(x)\geqslant 1\). Donc l'équation \(f(x)=0\) n'admet pas de solutions sur cet intervalle.
Sur l'intervalle \([0;2[\), d'après le tableau de variations, la fonction est continue et strictement décroissante.
De plus, \(0\in ]-\infty ;2]\)
Donc d'après le TVI, l'équation \(f(x)=0\) admet exactement une solution sur cet intervalle.
Sur l'intervalle \(]2;+\infty[\), d'après le tableau de variations, la fonction est continue et strictement croissante.
De plus, \(0\in ]-\infty ;1]\)
Donc d'après le TVI, l'équation \(f(x)=0\) admet exactement une solution sur cet intervalle.
Ainsi, au total, l'équation \(f(x)=0\) admet exactement deux solutions dans \(\mathbb R \backslash \{2\}\)