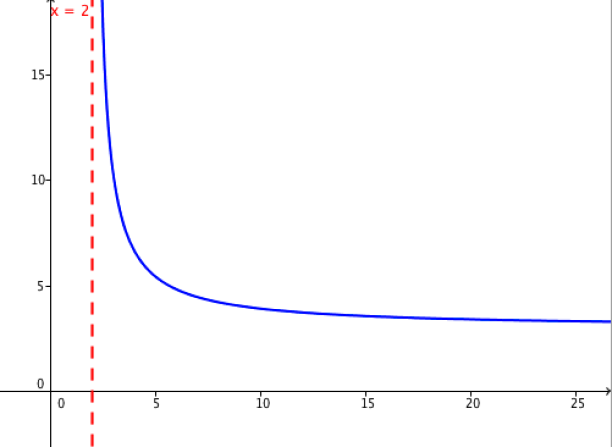
On considère à nouveau la fonction définie sur \(]2 ;+\infty[\) par \(f :x\longmapsto \frac{9x+4}{3x-6}\)
Mais cette fois-ci, nous allons étudier son comportement au voisinage de la valeur interdite 2.
Question
Calculer \(f(2,1)\), \(f(2,01)\), \(f(2,001)\), \(f(2)\).
Faire une conjecture sur le comportement de \(f\) aux alentours de 2.
Solution
\(f(2,1)\approx 76,3\)
\(f(2,01)\approx 736,3\)
\(f(2,001)\approx 7336,3\)
\(f(2)\) n'est pas défini !
Il semblerait donc que lorsqu'on s'approche de 2, par valeur supérieure, la fonction \(f\) tende vers +∞.
Attention :
Bien faire attention ici à l'ensemble de définition : on a \(x>2\) compte tenu de l'intervalle donné au départ.
Cela est important dans le cas de notre fonction car si on s'approche de 2 par valeur inférieure, la limite est -∞ !
Cette conjecture ne constitue en rien une preuve. Néanmoins, si elle est vraie, cela signifie qu'on peut obtenir des valeurs arbitrairement grandes en s'approchant suffisamment de 2. Vérifions cela à l'aide d'un algorithme :
S prend la valeur 10000
X prend la valeur 2,1
N prend la valeur 1
Tant Que f(x)<S
... N prend la valeur N+1
... X prend la valeur 2+1/10^N
Afficher X
Question
Quel est le rôle de cet algorithme ? A quoi servent les variables ?
Expliquer le choix de la méthode utilisée.
Solution
Cet algorithme permet de savoir si on peut dépasser la valeur 10000 en s'approchant suffisamment de 2.
Dans cet algorithme S désigne le seuil à dépasser. X désigne un nombre de plus en plus proche de 2. Pour cela, X est calculé par la formule \(2+\frac{1}{10^N}\) où N est une variable entière qui augmente de 1 à chaque passage de boucle.
On s'approche ainsi de plus en plus de deux, par valeur supérieure. Les valeurs prises par X sont 2,1, 2,01, 2,001, 2,0001 etc...
Question
Programmer cet algorithme et donner la valeur obtenue en sortie.
\(f(x)\) peut-il dépasser 1000000 ?
Indice
On pourra utiliser la calculatrice ou le langage Python en ligne.
Solution
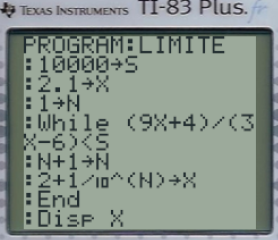
Le programme ci-dessus, ou ci-contre en langage TI, retourne la valeur 2,0001
Peut-on dépasser 1000000 ?
En initialisant la variable S à 1000000, on obtient en sortie X=2,000001. Il est donc possible de dépasser 1000000 et on imagine bien que quelque soit la taille du nombre choisi, en s'approchant suffisamment de 2, il sera possible de dépasser ce seuil.
Question
Interpréter graphiquement ce résultat
Indice
On pourra chercher l'équation d'une asymptote correspondant à cette limite que l'on vient de conjecturer.
Solution
Plus on x s'approche par la droite de la valeur interdite 2, plus f(x) grimpe vers l'infini.
La droite verticale d'équation \(x=2 \) est donc une asymptote verticale à la courbe \(\mathcal C_f\) dans la mesure où la courbe s'en approche sans jamais l'atteindre, x=2 étant une valeur interdite pour la fonction f.