Lire et interpréter un tableau de variations
On considère une fonction f dont le tableau de variations est donné ci-dessous. On note \(\mathcal C_f\) sa courbe représentative.
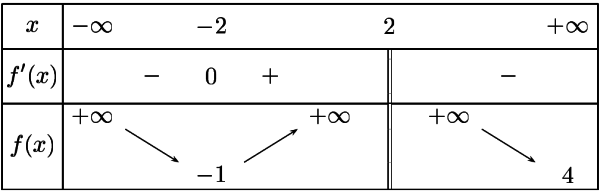
Question
Quel est l'ensemble de définition de la fonction f ?
Solution
f est définie sur \(]-\infty ;2[ \cup ]2 ;+\infty[\)
Question
Quelles sont les limites données dans le tableau ? Les écrire en utilisant la notation mathématique.
Solution
\(\lim\limits_{x \to -\infty } f(x)=+\infty\)
\(\lim\limits_{x \to 2 } f(x)=+\infty\)
\(\lim\limits_{x \to +\infty } f(x)=4\)
Question
Quelles sont les asymptotes à la courbe \(\mathcal C_f\)
Solution
La première limite ne donne pas lieu une asymptote. C'est une limite infinie en l'infini.
La seconde limite : \(\lim\limits_{x \to 2 } f(x)=+\infty\) est une limite infinie en un point fini. Elle donne lieu à une asymptote verticale d'équation \(x=2\)
La dernière limite : \(\lim\limits_{x \to +\infty } f(x)=4\) est une limite finie en l'infini. Elle donne lieu à une asymptote horizontale d'équation \(y=4\)
Question
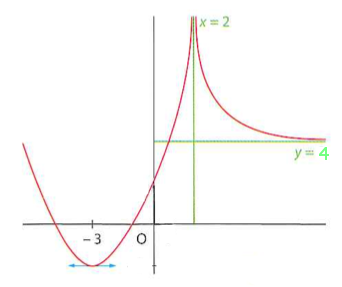
Donner une courbe représentative possible de la fonction f