Activité d'approche
Question
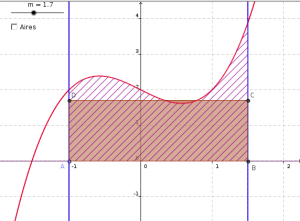
A l'aide de la figure ci-dessus, donner intuitivement une estimation de la valeur de m à choisir pour obtenir l'égalité des aires sous la courbe et du rectangle ABCD.
Solution
L'exemple choisi avec 1,7 donne visiblement une aire de ABCD trop petite.
Si on choisit m=2,5, l'aire de ABCD sera visiblement trop grande.
La bonne valeur doit se situer entre les deux. On peut conjecturer une valeur environ égale à 2,2.
Question
A l'aide de la simulation ci-dessous, faire varier la valeur de \(m\) à l'aide du curseur pour affiner votre conjecture. Affichez ensuite les valeurs des aires pour vérifier la valeur trouvée.
Solution
avec \(m=2,1\), l'aire de ABCD vaut 5,25
avec \(m=2,2\), l'aire de ABCD vaut 5,5
l'aire sous la courbe est évaluée par géogébra à 5,39, donc la valeur de \(m\) cherchée se situe entre 2,1 et 2,2.
Nous allons à présent vérifier par le calcul cette conjecture.
Question
Calculer la valeur exacte le l'aire \(\mathcal A\) sous la courbe.
Vérifiez votre calcul à l'aide de la calculatrice.
Indice
Il s'agit de calculer \(\displaystyle \int_{-1}^{1,5} x^3-x+2~dx\).
Indice
Pour une fonction polynôme, il n'est pas compliqué de déterminer une primitive...
Solution
D'après les formules du cours, \(F(x)=\dfrac{x^4}{4}-\dfrac{x^2}{2}+2x\) est une primitive de f
\(F(-1)=\dfrac{1}{4}-\dfrac{1}{2}-2=\dfrac{-9}{4}\)
\(F(\dfrac{3}{2})=\dfrac{3^4}{2^4\times 4}-\dfrac{3^2}{2^2\times 2}+2\times \dfrac{3}{2}=\dfrac{201}{64}\)
Donc \(\displaystyle \int_{-1}^{1,5} x^3-x+2~dx=\dfrac{201}{64}-\left(-\dfrac{9}{4}\right)=\dfrac{345}{64}\approx 5,39\)
Pour les calculs exacts avec les fractions, vous pouvez vous aider des fonctions de calcul sur les fractions de vos calculatrices.
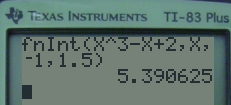
Il est toujours utile de vérifier la valeur approchée obtenue avec sa calculatrice au moyen de la fonction de calcul numérique d'intégrales.
Question
En déduire la valeur de \(m\) pour que l'aire de ABCD soit égale à l'aire \(\mathcal A\) sous la courbe.
Indice
L'aire du rectangle est Longueur x largeur. La longueur est donnée. L'aire finale aussi.
Solution
On a \(\mathcal A=AB\times m\) donc \(m=\dfrac{\mathcal A}{AB}\approx \dfrac{5,39}{2,5}\approx 2,15\).
La valeur de m cherchée est de 2,15 environ, ce qui est conforme à la conjecture initiale.
Question
Exprimer en fonction des données de départ (intervalle\( [a ;b]\) et fonction \(f\)) la formule permettant de calculer directement cette valeur de \(m\).
Indice
Nous avons trouvé \(m=\dfrac{\mathcal A}{AB}\).
Solution
L'aire \(\mathcal A = \displaystyle \int_{a}^{b} f(x)~dx\)
La longueur \(AB=b-a\)
On en déduit que la valeur de \(m\) se calcule par la formule \(m=\dfrac{\displaystyle \int_{a}^{b} f(x)~dx}{b-a}=\dfrac{1}{b-a}\displaystyle \int_{a}^{b} f(x)~dx\)