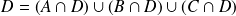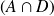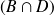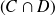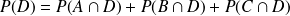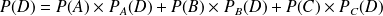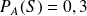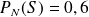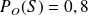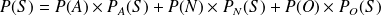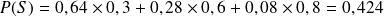Formule des probabilités totales
Rappel :
On se rappelle de cette formule de la classe de seconde sur la probabilité de l'union de deux événements.
Le cas particulier en cas d'événements disjoints s'applique très bien à la situation d'une partition de l'univers en plusieurs événements.
Supposons que l'univers Ω possède une partition en trois événements A, B et C et que nous connaissons les probabilités conditionnelles d'un événement D sachant A, B et C. On sait :
Donc
Par conséquent
|  |
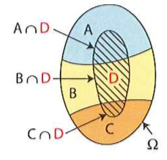Par conséquent on peut calculer la probabilité d'un événement sachant ses probabilités conditionnelles relatives à une partition de l'univers.
Méthode : Traduction sur un arbre pondéré
Sur un arbre pondéré, la probabilité d'un événement D associé à plusieurs feuilles est égale à la somme des probabilités de chacune de ces feuilles.
Exemple :
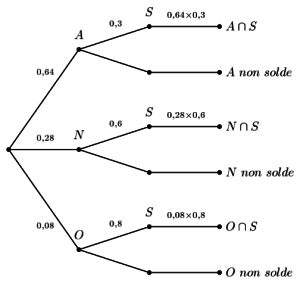
Un magasin de sport propose des réductions sur les 3 marques qu'il distribue.
La marque A représente 64% des ventes, la marque N représente 28% et la marque O représente 8%.
On sait que sont soldés 30% des vêtements de la marque A, 60% de la marque N et 80% de la marque O.
Quel pourcentage au total des vêtements vendus par ce magasin est soldé ?
On sait que les événements A, N et O représentent une partition de l'univers Ω des vêtements vendus car
un vêtement ne peut pas être de deux marques à la fois
il n'y a pas d'autre marque en magasin puisque 64%+28%+8%=100% des vêtements.
 | On connaît les probabilités conditionnelles pour chacune des marques relatives au soldes :
On en déduit la probabilité qu'un article soit soldé par la somme
Donc
Par conséquent 42,4% des vêtements vendus par ce magasin sont soldés. |
