Somme et coordonnées
Dans un repère on donne les points :
A(1 ;2)
B(-1 ;-1)
C(5 ;4)
Question
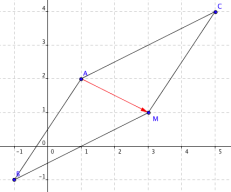
Déterminer les coordonnées du point M, 4ème sommet du parallélogramme ABMC.
Indice
Une méthode consiste à utiliser la règle du parallélogramme.
Indice
On pourra calculer la somme \(\overrightarrow{AB}+\overrightarrow{AC}\).
Solution
D'après la règle du parallélogramme, le point M est tel que \(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}\).
Nous allons tout d'abord calculer les coordonnées de \(\overrightarrow{AM}\).
\(x_B-x_A=-1-1=-2\) et \(y_B-y_A=-1-2=-3\)
donc \(\overrightarrow{AB} \left (\begin{array}{c}-2\\-3\end{array}\right )\).
\(x_C-x_A=5-1=4\) et \(y_C-y_A=4-2=2\)
donc \(\overrightarrow{AB} \left (\begin{array}{c}4\\2\end{array}\right )\).
En ajoutant les coordonnées de ces deux vecteurs on en conclut que \(\overrightarrow{AB}+\overrightarrow{AC} \left (\begin{array}{c}2\\-1\end{array}\right )\). Ce sont donc aussi les coordonnées de \(\overrightarrow{AM}\).
Déterminons à présent les coordonnées de M
Si on note \(M(x_M ;y_M)\) on peut
d'une part dire que \(\overrightarrow{AM} \left (\begin{array}{c}x_M-1\\y_M-2\end{array}\right )\),
d'autre part \(\overrightarrow{AM} \left (\begin{array}{c}2\\-1\end{array}\right )\).
Par identification, on obtient deux équations nous donnant les coordonnées de M cherchées :
\(x_M-1=2\) donc \(x-M=3\)
\(y_M-2=-1\) donc \(y_M=1\)
En conclusion, le point M cherché a pour coordonnées M(3 ;1).